The Law of Biot Savart¶
This handy little law is the foundation upon which most of the air core coil formulas in this site are based.
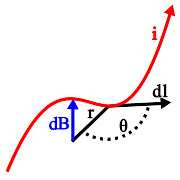
$d \mathbf B = \frac {\mu_o i} {4\pi} \frac {d \mathbf l \sin \theta} {r^2}$
The current element $d \mathbf l$ on a current filement with current i contributes a magnetic field, $d \mathbf B$, in a direction normal to the plane formed by $d \mathbf l$ and the vector r.
The good news is that by solving this integral for an arbitrary configuration of current filaments (like a coil, or set of coils) you can compute the magnetic field vector at any point in space.
The bad news is that there is no closed solution to this integral for most interesting configurations of current filaments and vectors r.
Oh well.
Magnet Formulas, © 2018 by Eric Dennison. Source code and License on Github