On-Axis Field of a Finite, Straight, Thin Shell Solenoid¶
This formula uses the formula for the field due to a current loop, integrated over a range of axial displacements to obtain the magnetic field at any point on the axis of a finite, thin shell solenoid.
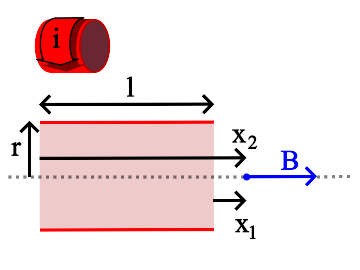
$B = \frac {\mu_o i N}{2 l} \left [ \frac {x_2} {\sqrt{x_2^2 + r^2}} - \frac {x_1} {\sqrt{x_1^2 + r^2}}\right ]$
B is the magnetic field, in teslas, at any point on the axis of the solenoid. The direction of the field is parallel to the solenoid axis.
$\mathbf \mu_o$ is the permeability constant (1.26x10-6 Hm-1)
i is the current in the wire, in amperes.
N is the total number of turns of wire in the solenoid.
l is the length of the solenoid, in meters.
r is the radius of the solenoid, in meters.
x1 and x2 are the distances, on axis, from the ends of the solenoid to the magnetic field measurement point, in meters.
Special Case: x1 = -x2¶
$B = \frac {\mu_o i N}{\sqrt{l^2 + 4 r^2}}$
The magnetic field measurement point is at the center of the solenoid.
Magnet Formulas, © 2018 by Eric Dennison. Source code and License on Github